Python を用いて迷路の最善手を方策勾配法で強化学習

迷路を解くためのモデル生成

　こちらの続きで、Deep-Reinforcement-Learning-Book/program/2_2_maze_random.ipynb at master · YutaroOgawa/Deep-Reinforcement-Learning-Book · GitHub を参照しながら強化学習で迷路を解くモデルの生成と可視化を実装する。

迷路の定義とその表現

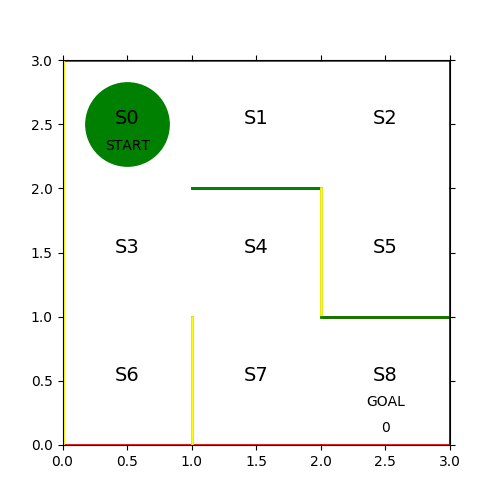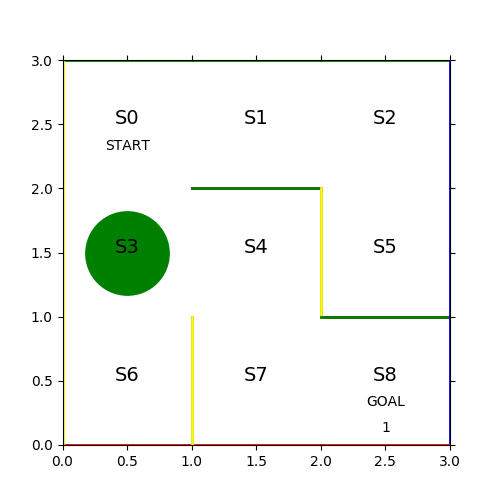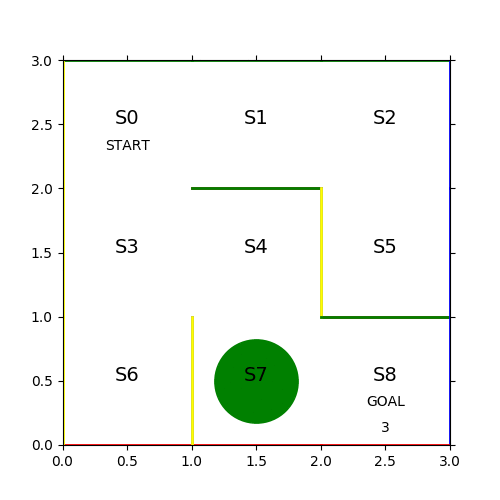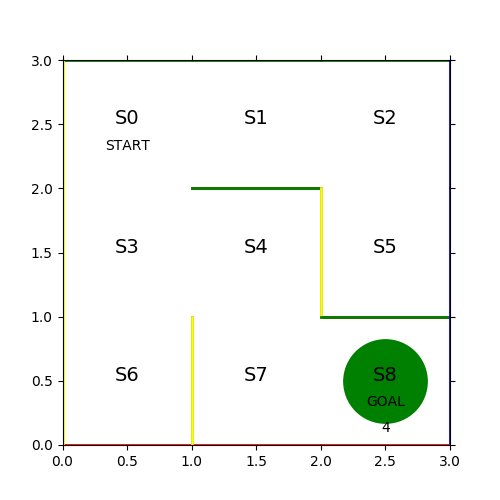
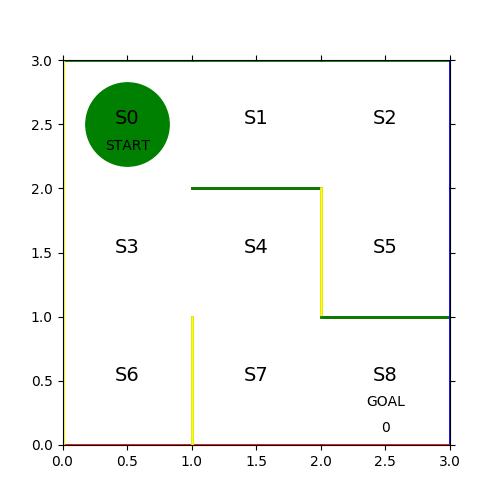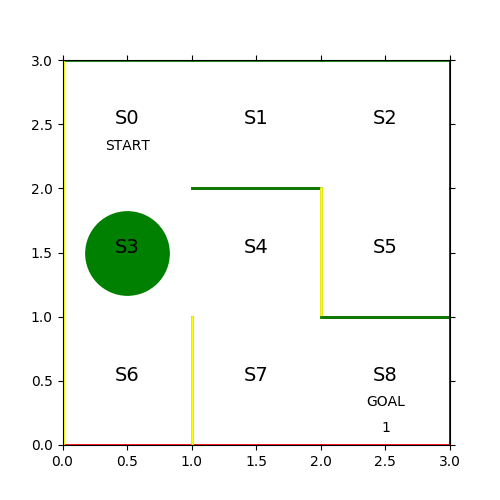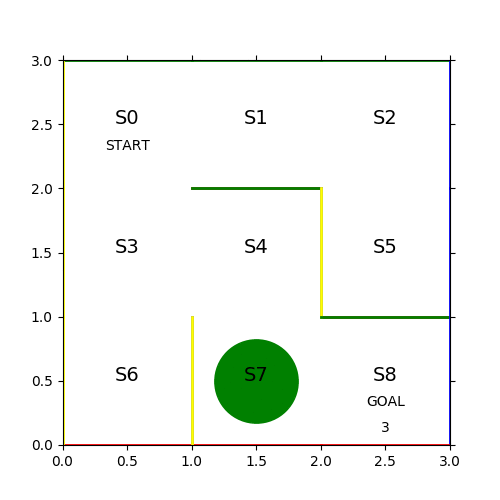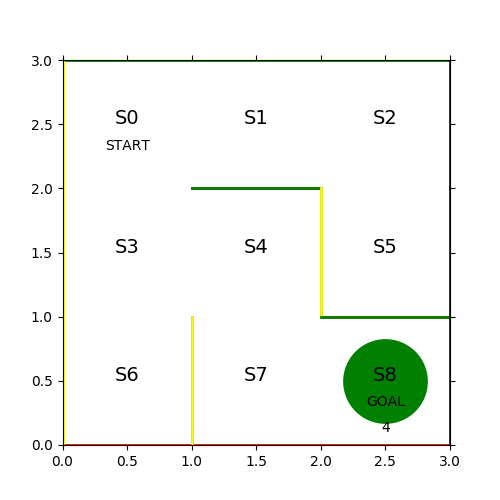
　課題を解くのに当たって、今回取り扱う迷路の定義を確認する。

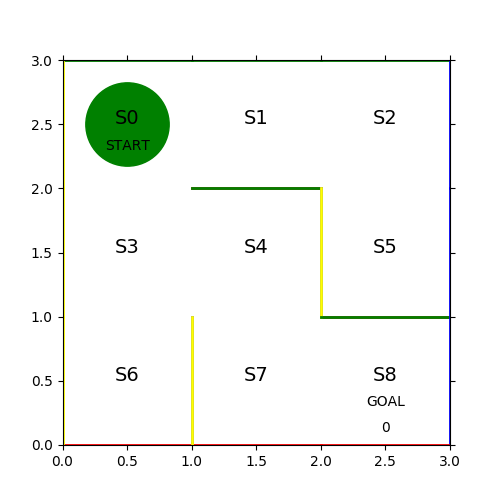
コマは左上の S0 マスからスタートして、右下の S8 マスでゴールとする
コマは1ステップごとに上下左右の1マスづつ移動する
各マスには固定の壁があり、壁を通り抜けることはできない
プレイヤーは S8 以外のマスに入ったら次のステップには出なくてはいけない

　例えば、START 地点においては右か下に移動すると「行動」が実行可能であるが、この移動可能性を [ 上, 右, 下, 左 ] の順に [ 0, nan, nan, 0 ] としてベクトル定義する。そして各マスを「状態」として、その「状態」における移動可能性をパラメータ行列 θ で定義する。

    theta = numpy.array([
        [numpy.nan, 1,          1,          numpy.nan], 
        [numpy.nan, 1,          numpy.nan,  1        ],
        [numpy.nan, numpy.nan,  1,          1        ],
        [1,         1,          1,          numpy.nan],
        [numpy.nan, numpy.nan,  1,          1        ],
        [1,         numpy.nan,  numpy.nan,  numpy.nan],
        [1,         numpy.nan,  numpy.nan,  numpy.nan],
        [1,         1,          numpy.nan,  numpy.nan],
        [numpy.nan, numpy.nan,  numpy.nan,  1        ],
    ])

　行動によって状態 S0 から右に移動したら S1、S0 から下に移動したら S3 に状態遷移するといったオフセットが定式化できる。

    next_state_offset = (-3, 1, 3, -1)

　これを利用することで、アクション状態遷移をスカラー値で計算できるようになる。

    def initMazePlot(self):
        figure = pyplot.figure(figsize=(5, 5)) 
        axes = figure.add_subplot(111) 

        axes.text(0.5, 2.3, 'START', ha='center')
        axes.text(2.5, 0.3, 'GOAL', ha='center')
        [m, n] = self.maze.shape
        for sidx in range(0, m):
            x = (sidx % 3)
            y = 3 - int(sidx / 3)
            axes.text(x + 0.5, y - 0.5, f'S{sidx}', size=14, ha='center')

            for aidx in range(0, n):
                if not(numpy.isnan(self.maze[sidx][aidx])):
                    continue
                if aidx == 0:
                    axes.plot([x, x+1], [y, y], color='green', linewidth=2)
                elif aidx == 1:
                    pyplot.plot([x+1, x+1], [y, y-1], color='blue', linewidth=2)
                elif aidx == 2:
                    axes.plot([x, x+1], [y-1, y-1], color='red', linewidth=2)
                elif aidx == 3:
                    axes.plot([x, x], [y, y-1], color='yellow', linewidth=2)

　また元のプログラムだと直に線やテキストを書いていて面倒なので、パラメータ行列 θ から状態や線を書き出すようにした。

softmax 関数で方策を実装

　強化学習では行動を定めたルールを方策（ Policy ）と呼び、「π(状態, 行動) 」で表現する。方策 π はパラメータ行列 θ から変換された「状態Sの場合に行動Aを取る確率」となる。今回は softmax 関数を用いて θ を π に変換する。

def convertPi(theta):
    beta = 1.0
    [m, n] = theta.shape
    pi = numpy.zeros((m, n))
    exp_theta = numpy.exp(beta * theta)
    for i in range(0, m):
        pi[i][:] = exp_theta[i][:] / numpy.nansum(exp_theta[i][:])
    return numpy.nan_to_num(pi)

　生成した π を用いた確率で 0=上, 1=右, 2=下, 3=左の行動を決定。行動後の状態遷移を戻す。

def next(pi, state):
    next_state_offset = (-3, 1, 3, -1)
    action = numpy.random.choice(a=list(range(0, 4)), p=pi[state, :])
    return [action, state + next_state_offset[action]]

　softmax 関数の数学的な証明などについて厳しいが、下記記事において直感的な理解がある程度まではできた。

　1回目の実行では θ の各状態において取りうる行動確率を等分した π が生成されるため、実態的にはランダムに動作する。

[[0.    0.5   0.5   0.   ]
 [0.    0.5   0.    0.5  ]
 [0.    0.    0.5   0.5  ]
 [0.333 0.333 0.333 0.   ]
 [0.    0.    0.5   0.5  ]
 [1.    0.    0.    0.   ]
 [1.    0.    0.    0.   ]
 [0.5   0.5   0.    0.   ]
 [0.    0.    0.    1.   ]]

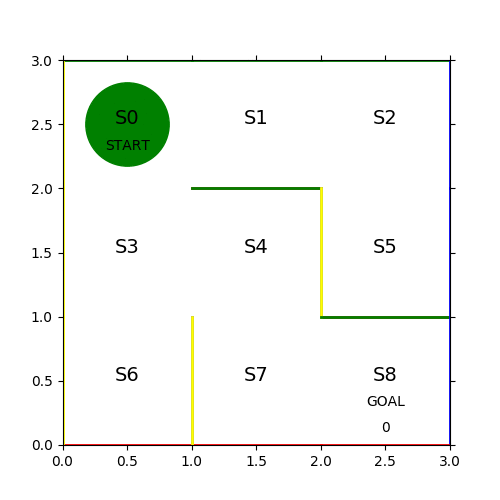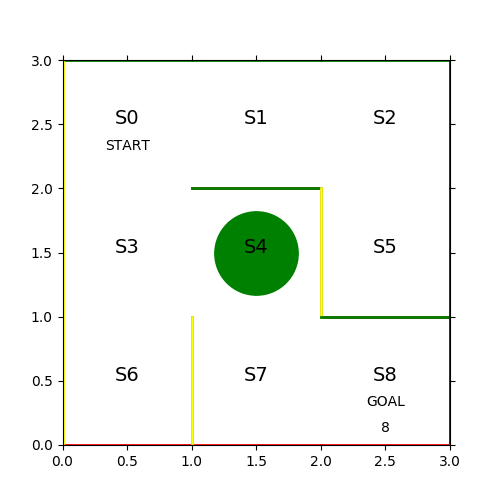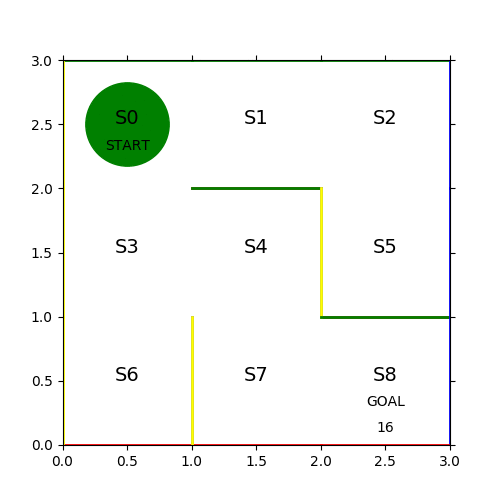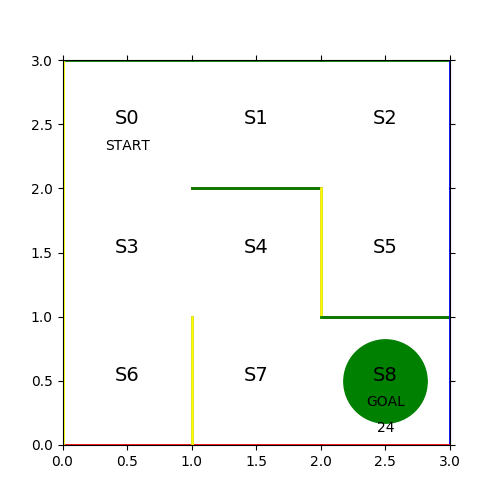
　見事な千鳥足で24ステップかかっている。各ステップのヒストリーを保存して次の学習に活かす。

方策勾配法を用いて方策を更新

　方策勾配法では下記の式に従ってパラメータ θ を更新する。

θ(s, a) = θ(s, a) + 学習係数 x Δθ(s, a)
Δθ(s, a) = { 採用回数(s, a) + 現在の方策での確率(s, a)  x 状態sで何らかの行動をした回数 } / 掛かったステップ数

　これは S8 に至るまでのステップ数が少ない場合に、Δθ(s, a) の報酬が高くなり、ステップ数が多くなるほど報酬が低くなるため、有効な「状態」と「行動」の組み合わせになるほど選択する確率が高くなっていく。

def updateTheta(theta, pi, history):
    eta = 0.2
    t = len(history) - 1
    [m, n] = theta.shape
    delta_theta = theta.copy()

    for sidx in range(0, m):
        state_num = len([sa for sa in history if sa['state'] == sidx])
        for aidx in range(0, n):
            if numpy.isnan(theta[sidx][aidx]):
                continue
            action_in_state_num = len([sa for sa in history if sa['state'] == sidx and sa['action'] == aidx])
            delta_theta[sidx][aidx] = (action_in_state_num + pi[sidx][aidx] * state_num) / t
    return theta + eta * delta_theta

　これを繰り返す事でステップ数ができる限り少なくなるように学習させる。学習に伴って θ が変更されれば π もそれに合わせて変化していくが、変化量が少なくなった場合に収束したとみなして学習を終了させる。

    pi = convertPi(theta)
    lerning = []
    for i in range(0, 1000):
        history = goalMaze(pi)
        if i == 0:
            print(f'step: {i+1}')
            print(pi)
            plot.execute(history)

        lerning.append({'step': i+1, 'result': len(history) - 1})
        theta = updateTheta(theta, pi, history)
        new_pi = convertPi(theta)

        if numpy.sum(numpy.abs(new_pi - pi)) > 10 ** -5:
            pi = new_pi
        else:
            print(f'step: {i+1}')
            print(new_pi)
            plot.execute(history)
            break

　学習した結果。今回は 164回で収束した。

　最終的なπは以下の通り。

[[0.    0.    1.    0.   ]
 [0.    0.36  0.    0.64 ]
 [0.    0.    0.494 0.506]
 [0.    1.    0.    0.   ]
 [0.    0.    1.    0.   ]
 [1.    0.    0.    0.   ]
 [1.    0.    0.    0.   ]
 [0.    1.    0.    0.   ]
 [0.    0.    0.    1.   ]]